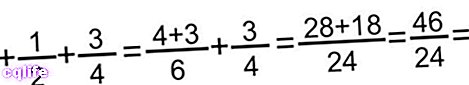Vysvětlíme, co je to sčítání nebo sčítání v matematice, jeho historii, vlastnosti a příklady. Také metody pro sčítání zlomků.

jaký je součet?
Sčítání nebo sčítání je základní matematická operace, která spočívá v začlenění nových prvků do a soubor numerické, tedy ke sloučení dvou čísel k získání nového, které vyjadřuje celkovou hodnotu dvou předchozích. Sčítání je základní princip, se kterým se učíme spojovat s čísly, protože pouhý fakt počítání po jednom (1, 2, 3, 4 ...) zahrnuje sčítání 1 (1 + 0, 1 + 1, 1 + 2, 1 + 3…).
Součet je operace aritmetického typu, která umožňuje kombinovat čísla různých typů: přírodní, celá číslazlomky, reálné, racionální, iracionální a komplexní, stejně jako struktury s nimi spojené, jako jsou vektorové prostory nebo matice. Na algebra Modernismus je reprezentován symbolem +, vloženým mezi prvky, které mají být přidány, a vyjádřený slovně jako „více“: „1 + 1 = 2“ se čte „jedna plus jedna se rovná dvěma“.
Na druhou stranu prvky, které mají být přidány, jsou známé jako „sčítání“ a číslo získané na konci se nazývá „výsledek“.
Historie součtu
Sčítání je jednou z nejstarších a nejzákladnějších známých matematických operací. Má se za to, že lidská bytost Již od neolitu ovládal elementární matematické principy, mezi nimiž by nutně bylo sčítání a odčítání, protože tyto operace lze snadno doložit při zemědělských zásobách, které se zvyšovaly a snižovaly podle ročního období.
Studium sčítání a jeho aplikace na přirozená i zlomková čísla však začalo u starých Egypťanů a pokračovalo ve složitějším vývoji u Babyloňanů, a zejména u Číňanů a Hindů, kteří jako první začali čísla sčítat. . Ale pouze v renesance bankovní boom zavedl součet desetinných míst a vulgárních logaritmů.
Vlastnosti součtu
Sčítání jako matematická operace má sadu vlastností, kterými jsou:
- Komutativní vlastnost. Stanoví, že pořadí sčítání nemění výsledek, to znamená, že a + b je přesně totéž jako b + a a v obou případech je získán stejný výsledek.
- Asociativní vlastnost. Stanovuje, že při přidávání tří nebo více prvků je možné seskupit dva z nich a vyřešit je jako první, bez ohledu na to, jaké jsou, aniž by se změnil konečný výsledek. To znamená, že pokud chceme sečíst a + b + c, můžeme si vybrat dva způsoby: (a + b) + c nebo a + (b + c), aniž by to ovlivnilo výsledek.
- Vlastnost identity. Stanoví, že nula je neutrální prvek v operaci, takže její přidání s jakýmkoli jiným číslem bude vždy mít za následek stejné poslední číslo: a + 0 = a.
- Uzavírací nemovitost. Stanoví, že výsledek součtu bude vždy patřit do stejné číselné množiny sčítání, pokud tyto součet sdílejí stejnou množinu. To znamená, že pokud sčítání a a b patří k N (přirozené), Z (celá čísla), Q (iracionální), R (reálné) nebo C (komplexní), bude výsledek součtu také patřit do stejné množiny.
Příklady sčítání
Zde je několik jednoduchých příkladů přidání:
- Žena má čtyři květiny, ale má narozeniny a dostane dalších osm. Kolik květin má na konci dne? 4 květy + 8 květů = 12 květů.
- Pastýř má 15 ovcí, zatímco jeho kolega 13. Pokud se rozhodnou sloučit svá stáda, kolik ovcí bude mít celkem? 15 ovcí + 13 ovcí = 28 ovcí.
- Jabloň dává svému majiteli 5 jablek měsíčně. Kolik jablek bude mít na konci jednoho roku? Protože rok je 12 měsíců, musíme přidat 5 dvanáctkrát, přičemž použijeme asociativní vlastnost: (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + ( 5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 jablek za rok.
Součet zlomků
Při sčítání zlomků jsou různé metody které můžeme použít k získání výsledku v závislosti na tom, zda se jedná o správné, nesprávné a smíšené zlomky.
- Metoda sčítání zlomků se stejným jmenovatelem. Toto je nejjednodušší případ, ve kterém jednoduše sečteme čitatele a ponecháme stejný jmenovatel. Například:
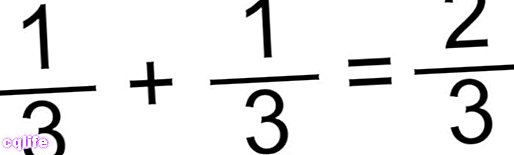
nebo
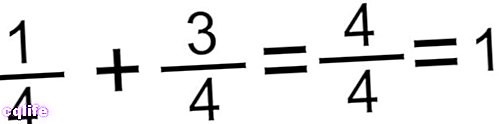
- Motýlí metoda. Tato metoda nám umožňuje sčítat jakýkoli typ zlomků s různými jmenovateli, jednoduše vynásobíme čitatele prvního jmenovatelem druhého a naopak a poté sečteme součiny (pro získání čitatele) a poté vynásobíme jmenovatele, abychom získali jmenovatel konečného zlomku. Jakmile jsou tyto operace provedeny, často budeme muset snížit výsledek. Například:
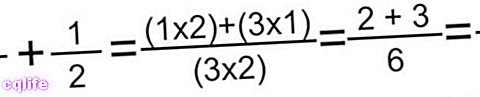
- Metoda přidávání tří frakcí. V tomto případě jednoduše přidáme první dva a k výsledku přidáme poslední, přičemž použijeme předchozí metodu a v případě potřeby výsledek zmenšíme nebo zjednodušíme. Například: